Intro

In the previous sections, we explored the fundamentals and applications of traditional state space models (SSMs), revealing their versatility in handling complex temporal dynamics. However, a persistent challenge with these "vanilla" models is their susceptibility to the vanishing and exploding gradients problem—particularly when applied to long data sequences. This complicates training and limits the potential depth and accuracy of these models. Indeed, a new class of models, known as S4 (Structured State-space Models for Sequences), has emerged to address these shortcomings. S4 models incorporate advanced architectural innovations that stabilize the training process and enhance model performance across extensive sequences. This chapter delves into the mechanics of S4 models, illustrating how they effectively counter the gradient issues that plague their traditional counterparts and why they represent a significant advancement in the field of sequential data analysis.

The memory problem and the S4 model

Bearing in mind the fundamental equations of discrete SSMs:

$$ h_{n}=Ah_{n-1}+Bx_n,\ \ y_n = Ch_n+Dx_n $$

we can see that the vector h_n carries the information extracted from the input sequence 𝑥 up to the current time n. This remark lets us interpret the internal state as the system's memory. Indeed, every new data point x_n influences the next stage of the memory being “gated” by the input matrix B and then added to the memory, including its piece of information within the history recorded by h_n. Moreover, the matrix A describes the evolution of the memory through time, selecting the parts of it that need to be forgotten to allocate the information content of the more recent entries.

This very intuitive formulation again recalls the RNNs formalization, and, unfortunately, the parallel between the two also involves the issues we know from recurrent models, such as exploding or vanishing gradients. Indeed, the elegant formulation of the SSM layer we delved into in the previous chapter actually reported poor results in practice. However, the Albert Gu, Tri Dao, and Christopher Ré team at Stanford University studied this problem in recent years and came up with a novel solution that allows the state to better remember the past.

Happy Happy Hippo!

As evident from the preceding discussion, the matrix A plays a crucial role in determining the memory retention capabilities of the state. A key innovation introduced by the researchers Albert Gu and Christopher Ré in their exploration of the S4 model is the High Order Polynomial Projection Operator (HiPPO) theory, which systematically addresses the limitations of matrix A in conventional SSMs.

The HiPPO method fundamentally rethinks how the matrix A is structured, focusing on enhancing the model’s ability to handle long-range dependencies more effectively. Instead of a typical linear transformation that might excessively dilute information over time, HiPPO designs A to project the internal state onto a basis of orthogonal polynomials, encoding the input into the coefficients of Legendre Polynomials. This projection is mathematically optimized to maximize information retention over the course of an input sequence.

The HiPPO method defines a mathematical framework that allows A to operate as a continuous operator over a finite interval, effectively transforming it into a generator of a stable dynamical system. By projecting the state space onto a high-degree polynomial basis, HiPPO ensures that each component of the vector h_n encodes information at various temporal scales, from the most recent inputs to those far back in the sequence.

This orthogonal projection prevents the gradient problems commonly seen with deep or recurrent neural networks and provides a structured way to selectively remember and forget information. As a result, each element of the state vector h_n maintains a balance between capturing new data and preserving relevant historical details, thereby enabling the system to recall significant events or patterns over lengthy time horizons.

Implementing HiPPO within an SSM framework involves modifying the matrix A initialization to reflect polynomial terms that correspond to the desired memory characteristics. Indeed, in the vanilla SSM layer, all the matrices (i.e., layers’ parameters) were randomly initialized, and during the training phase, they are learned to solve the task at hand. The authors of this first paper provide the structure of the matrix A when initialized:

$$ \text{HiPPO Matrix}\ \ \ A_{i,j}=\begin{cases} (2i+1)^{\frac{1}{2}}(2j+1)^{\frac{1}{2}}, & i{<}j \\ i+1, & i=j \\ 0, & i>j \end{cases} $$

This approach is highly flexible; depending on the application, one can tweak the polynomial degree and the basis to tailor the memory decay and retention properties. Further, since after the application of the HiPPO initialization, the system is still Linear and Time-Invariant, it is still possible to take advantage of both the two discrete SSMs’ representations, namely the recurrent and the convolutional forms. This novelty, together with a novel and faster method to precompute the kernels in the convolutional representations, is presented in the Structured State-Space models for Sequences (S4) paper, which the authors also complement with several experiments on the Long-Range Arena (LRA) benchmark.

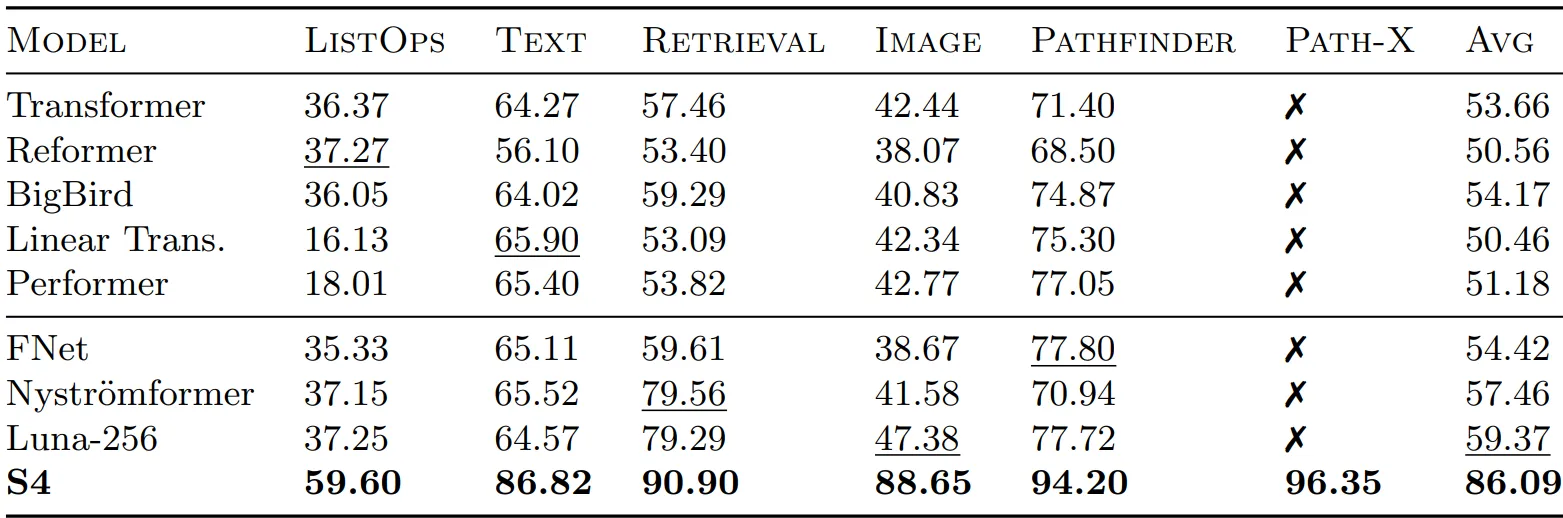
As can be seen from the table just reported, the S4 model marks a clear step forward in dealing with extremely long inputs, outperforming several (specialized) transformer-based models on every task and surpassing them by more than 30 p.p. on average. It is worth noting that the tasks within the LRA benchmark include different input modalities (e.g., text and images). Moreover, the S4 model succeeded in the PATH-X task, a challenging image task that transformer-based architectures cannot handle properly due to the extremely long context they have to deal with to make their own predictions.

The PATH-X task is a binary classification task where the models are fed with an image, including two dots and several dashed curves. The label is positive if a line connects the two dots, as in the figure above.

In general, the introduction of HiPPO into SSMs has shown remarkable improvements in various tasks that require processing long sequences, such as time series forecasting, speech recognition, and complex sequential reasoning. This has validated the theoretical underpinnings of HiPPO and demonstrated its practical efficacy across diverse domains.

The Mamba model

While the S4 model showed promising results and beat transformer-based architectures on challenging long-range tasks for the first time, they still report limitations in other tasks currently dominated by transformers. In particular, a free byproduct of the attention mechanism is selectivity. Since the context during the attention operation is not compressed, transformers can evaluate the importance of every token by directly comparing it with the others in the context window and later leverage these selected parts of the input to obtain the result. On the other hand, SSMs do not benefit from a similar property since it is Time-Invariant, as all the input tokens x_i are identically transformed by leveraging the same matrix B, which is constant regardless of the (semantic importance of the) input. For example, a task where S4 does not perform well is the selective copy, i.e., the task of copying or retrieving only and all the elements that match a certain condition. For example, we could provide the model with a sentence and require it to selectively copy only the nouns or the verbs.

In this case, we would our SSMs’ memory to choose if the new input represents something we need to remember (and, thus, add it to our memory content) or, instead, if we can overlook it, as we do not need it for the final output. Mamba aims to retain a compressed context (as opposed to the large context used by transformers), which is, however, structured and encodes only relevant pieces of information.

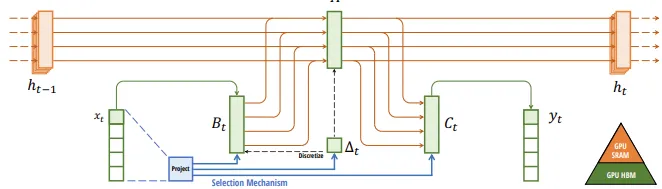
The Mamba model achieves selectivity by allowing B and C to be dynamic as opposed to the fixed (per iteration) A, B, C, and D defined in the vanilla SSM layer or in the S4 model. The matrices B=B(x) and C=C(x) within the Mamba layers depend now on the input, allowing for more context awareness. On the other hand, this modification makes the model not Time-Invariant, which, in turn, makes the precalculation of the convolutional kernel impossible. Thus, with this modification, we lose the possibility to use the SSM in the Convolutional representation. On the other hand, in the Mamba paper, the authors describe the parallel scan algorithm that allows for the parallelization of the scan operation by assuming the order in which we do operations does not matter. The parallel scan algorithm calculates the sequences in parts and iteratively adds them. These two novel features (the dynamicity of matrices B and C and the usage of the parallel scan algorithm) together represent the first novelty introduced in Mamba: the selective scan algorithm, making this model able to solve dynamic tasks such as the selective copy.

Gu et al. also introduce a second modification to speed up the computations of the model. This technical innovation regards the use of the GPU. Indeed, the authors find that the main bottleneck in Mamba’s computation comes from the frequent copying of data between the small but efficient SRAM and their larger but less efficient DRAM, since data, initially hosted in the DRAM, is copied on the SRAM for calculations, and the intermediate results are copied back to the DRAM. Their modification, dubbed kernel fusion, aims to avoid that many interactions between SRAM and DRAM, preventing to write the intermediate results on the DRAM, and directly making all the computations in the fast SRAM. In particular, they propose to have the Discretization, the Selective Scan, and the final multiplication with C in a single SRAM kernel, speeding up the Mamba’s operations. On the other hand, those intermediate results that were originally stored in the large and less efficient memory are critical for backpropagation. However, the authors find it more efficient to recalculate those during the backpropagation phase.

With these two modifications on the S4 model, Gu et al. presented this new and highly efficient architecture named Structured State-Space model with Selective Scan for Sequences (or S6), dubbed later on as Mamba for its hissing acronym reminiscent of the serpentine sound, echoing the model’s swift and powerful processing capabilities akin to the agility of a mamba snake.

Applications

The Mamba family of models has revolutionized sequence modeling by bridging the gap between the computational efficiency of state space models (SSMs) and the representational power required for diverse, high-dimensional data. Where traditional architectures like Transformers falter due to quadratic scaling or where convolutional neural networks struggle with long-range dependencies, Mamba models bring a refreshing balance of scalability, precision, and versatility.

What makes Mamba truly exceptional is its ability to adapt across vastly different domains, from generating lifelike human motions to synthesizing high-resolution images, all while maintaining a hardware-aware efficiency that unlocks previously unattainable possibilities. Below, we explore the groundbreaking applications of Mamba models in vision, motion modelling, audio, language, and generative modeling—showcasing how this innovative framework is reshaping the future of machine learning.

DiM: Diffusion Mamba for efficient high-resolution images

Diffusion Mamba (DiM) demonstrates the versatility of the Mamba architecture by applying it to high-resolution image synthesis in diffusion models, a task traditionally dominated by resource-intensive Transformer-based architectures. While Transformers face significant computational challenges due to quadratic scaling, DiM capitalizes on Mamba’s efficient state space model (SSM) design, repurposing it for two-dimensional image data. This adaptation underscores the power of Mamba as a scalable, hardware-aware sequence model capable of addressing diverse data structures.

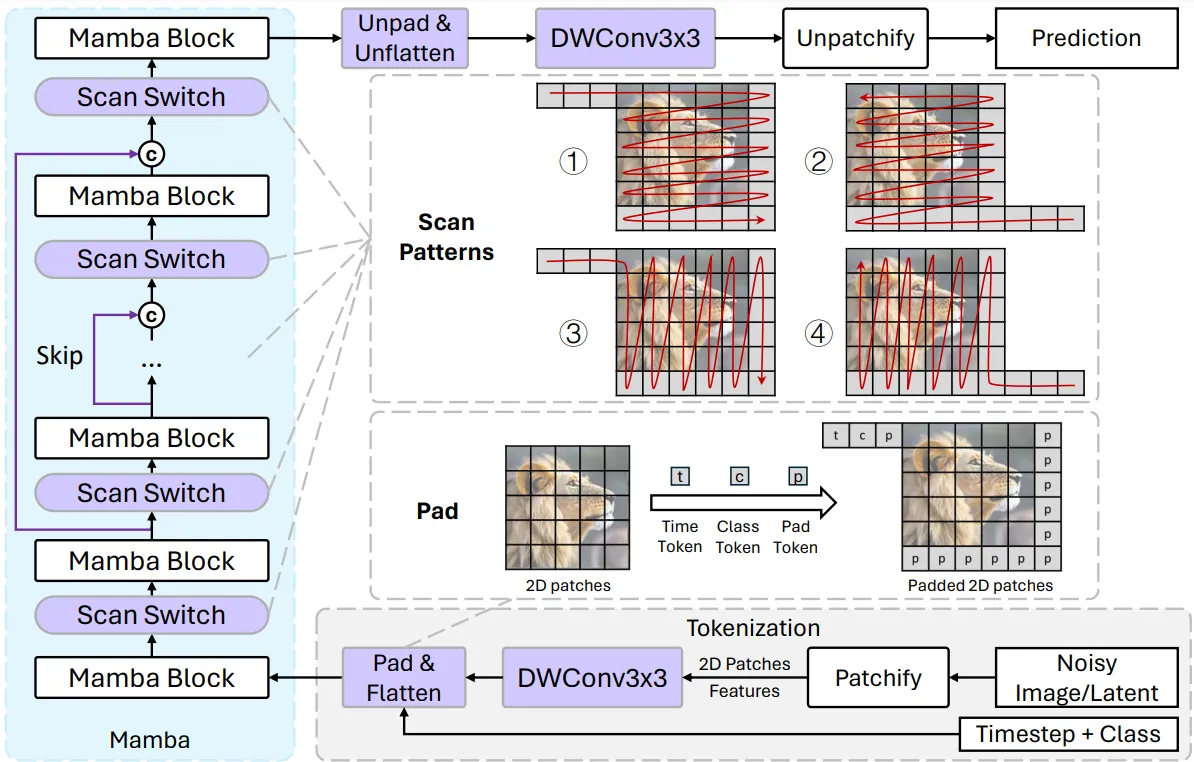
To adapt Mamba, which was initially designed for one-dimensional sequences, the authors introduced several key innovations:

• Multi-Directional Scanning Patterns: Instead of scanning image patches in a single direction (e.g., row by row), which limits the receptive field, DiM alternates between multiple scanning directions (e.g., row-major, reverse row-major, column-major, reverse column-major). This ensures that each patch can aggregate information from across the image, providing a more global understanding of the spatial structure.
• Learnable Padding Tokens: Flattening images into patch sequences often disrupts spatial continuity, as adjacent patches in the sequence may not be spatially adjacent. By appending learnable padding tokens at the ends of rows and columns, DiM helps the model recognize the boundaries and maintain awareness of the original image layout.
• Lightweight Local Feature Enhancement: To preserve the local continuity of image features, DiM incorporates lightweight depth-wise convolutional layers at both the input and output stages of the model. These layers reintroduce local spatial relationships lost during tokenization, ensuring that fine details are not neglected.

In addition to these architectural adaptations, DiM employs a "weak-to-strong" training strategy, pretraining on lower-resolution images before fine-tuning on higher resolutions, which reduces the computational burden. DiM also supports training-free upsampling, enabling the generation of ultra-high-resolution images without additional fine-tuning.

By combining Mamba’s efficiency with these specialized techniques, DiM achieves competitive performance in terms of FID-50K scores while significantly reducing computational costs compared to Transformer-based diffusion models. This work highlights Mamba’s potential as a foundational model for efficient, scalable, and high-quality image generation.

Motion Mamba: Efficient and Long Sequence Motion Generation

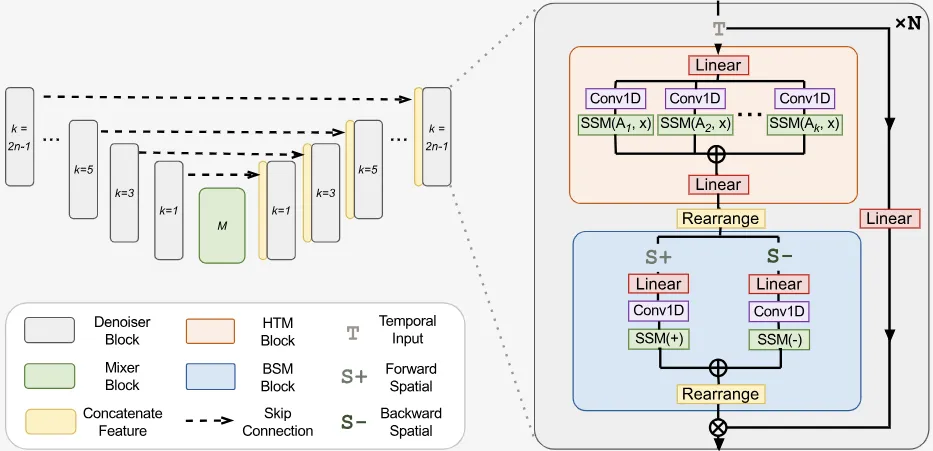
Motion Mamba extends the capabilities of the Mamba architecture to human motion generation, addressing the challenges of long-sequence modeling and computational efficiency in generative motion tasks. Motion generation inherently involves modeling sequences of human poses over time, where maintaining coherence and consistency across hundreds or even thousands of frames is essential for generating realistic motion. Akin to the previously discussed Diffusion Mamba paper, here motion generation is achieved with a diffusive process, but Motion Mamba leverages a latent diffusion framework, which operates on compressed latent representations to efficiently model complex data distributions. Furthermore, Motion Mamba introduces two novel components: the Hierarchical Temporal Mamba (HTM) block and the Bidirectional Spatial Mamba (BSM) block.

The HTM block organizes the temporal dimension hierarchically, processing motion frames with varying densities of scanning operations at different depths of the model. This means that lower-level features, which often encode richer and denser motion details, receive more frequent scanning operations, while higher-level features, which represent abstract and sparse motion patterns, are scanned less frequently. This strategy not only accommodates the diverse temporal dynamics of human motion but also reduces computational overhead by allocating resources proportionally to the complexity of the features being processed.

The BSM block addresses spatial coherence by rearranging and scanning latent representations bidirectionally, analyzing motion data from both forward and reverse perspectives. By swapping the temporal and channel dimensions during scanning, the BSM block ensures better flow of structural information across frames. This approach maintains a dense exchange of information within latent spaces, enabling the model to accurately capture skeleton-level features critical for generating realistic and temporally consistent motion sequences.

These innovations allow Motion Mamba to preserve motion consistency across frames and improve accuracy in temporal alignment. Compared to transformer-based diffusion models, Motion Mamba achieves up to 50% better FID scores and a fourfold increase in inference speed, as demonstrated on benchmarks like HumanML3D and KIT-ML. This pioneering integration of Mamba into motion generation showcases its potential for efficient, high-quality modeling of complex motion sequences.

Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model

Vision Mamba (ViM) explores the potential of Mamba as a generic backbone for vision tasks, addressing the computational inefficiencies and inductive biases of traditional architectures like Transformers and CNNs. Unlike hybrid approaches or convolution-based adaptations, ViM adopts a pure sequence modeling framework, processing images as flattened sequences of patches while leveraging bidirectional state space modeling to capture global visual context. To preserve spatial coherence, ViM incorporates positional embeddings and processes data bidirectionally within each block, enabling it to model high-resolution images without resorting to computationally expensive self-attention mechanisms.

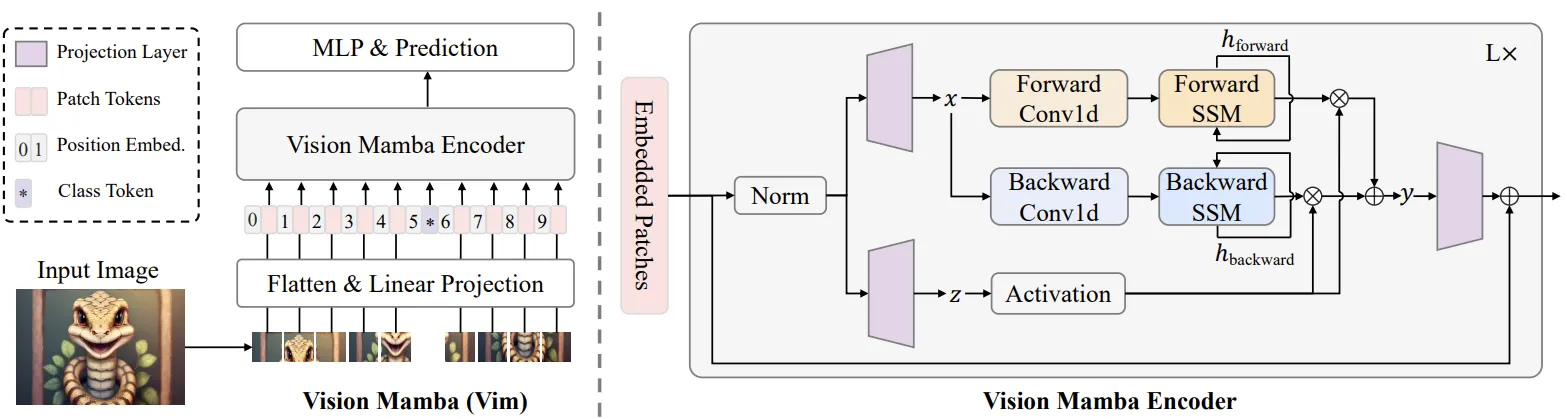
Resultswise, ViM outperforms well-established vision backbones like Vision Transformers (DeiT) and ResNet on tasks such as ImageNet classification, COCO object detection, and ADE20k semantic segmentation. For instance, Vim-Tiny achieves 2.8× faster inference and uses 86.8% less GPU memory compared to DeiT when processing 1248×1248 resolution images, while also demonstrating superior accuracy. These efficiency gains make ViM particularly suited for high-resolution applications, such as medical imaging and aerial analysis, where long sequence modeling is critical.

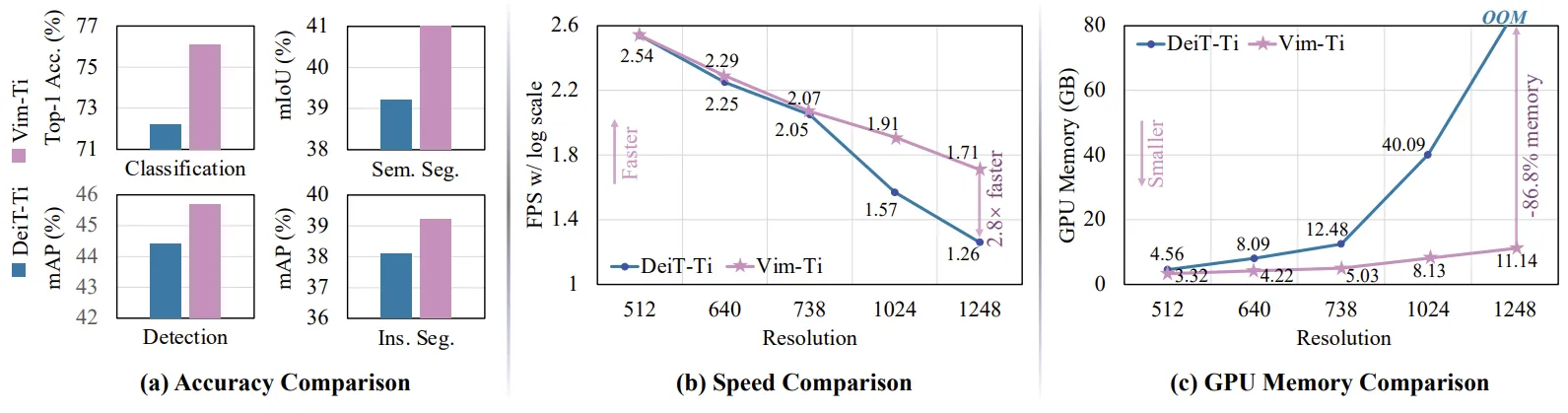
By maintaining linear scaling with sequence length and removing image-specific inductive biases, ViM establishes itself as a versatile and efficient backbone for next-generation vision models.

Audio Mamba: Bidirectional State Space Model for Audio Representation Learning

Audio Mamba (AuM) introduces a novel, self-attention-free architecture for audio classification, leveraging the efficiency of SSMs to address the computational challenges faced by transformer-based models. Traditional Audio Spectrogram Transformers (ASTs) particularly suffer from quadratic scaling, as the audio sequences are commonly very lengthy, making them expensive to encode. AuM replaces self-attention with bidirectional scanning, adapting the Mamba architecture for audio representation tasks. It processes audio spectrograms (which are provided as images to the model) by dividing them into square patches, embedding each patch into a sequence, and passing this sequence through a bidirectional Mamba encoder. This encoder processes data both forward and backward, ensuring spatial and temporal coherence while maintaining global context—similar to self-attention but significantly more efficient.

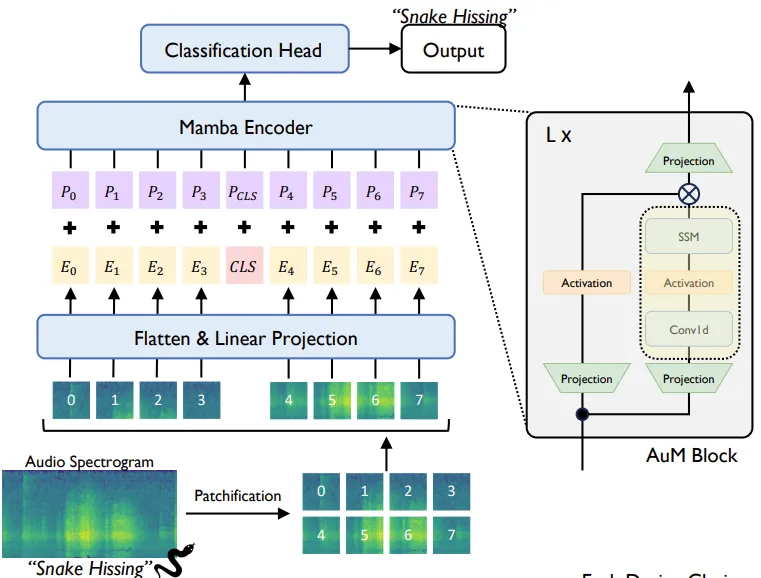
AuM also introduces an innovative use of classification tokens, strategically placed at the sequence midpoint, to optimize bidirectional processing. Experiments show that AuM achieves comparable or superior performance to ASTs across six audio classification benchmarks while being 1.6 times faster during inference and scaling linearly with sequence length. Its ability to handle long audio inputs with minimal memory consumption makes AuM a promising alternative for tasks requiring efficient audio representation, such as multimodal learning, audio-visual pretraining, and automatic speech recognition. This work demonstrates the potential of SSM-based architectures to redefine efficiency in audio processing.

Hymba: A Hybrid-head Architecture for Small Language Models

Hymba introduces a hybrid-head architecture for small language models, combining transformer attention mechanisms with Mamba-based state space models (SSMs) to balance high-resolution recall and efficient context summarization. The parallel fusion of attention and SSM heads allows Hymba to leverage the strengths of both: attention heads act as “snapshot memories”, capturing fine-grained details, while SSM heads function as “fading memories”, summarizing global context. This design avoids the bottlenecks of sequentially stacked modules and ensures efficient information processing across tasks.

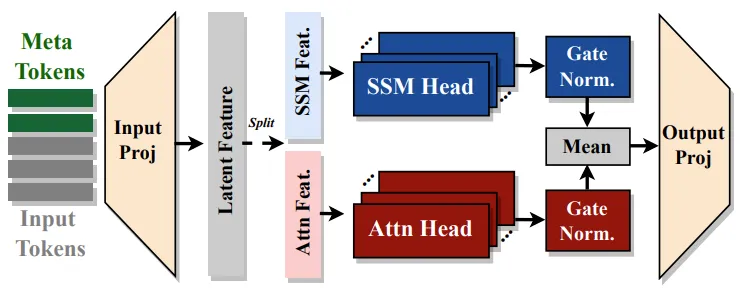
To enhance its efficiency, Hymba proposes several key innovations. Meta tokens, a set of learned embeddings prepended to inputs, act as a "learned cache," guiding attention to focus on relevant information and improving both memory and reasoning efficiency. These tokens redistribute attention, preventing the wasteful focus on initial tokens (e.g., BOS tokens) often seen in transformer models. KV cache optimization introduces a blend of local (sliding window) and global attention, reducing the memory and computational demands of traditional full attention. The inclusion of SSM heads further supports global context summarization, enabling more aggressive use of local attention without losing essential context. Together, these innovations reduce KV cache size by up to 4× and boost throughput by 3× while maintaining high task performance. With these advancements, Hymba achieves state-of-the-art results in both accuracy and efficiency, setting a new benchmark for small language models.

SeRpEnt: Selective Resampling for Expressive State Space Models

This work, produced by ItalAI, represents a theoretical advancement in the field of state space models SSMs, focusing on enhancing sequence compression and information efficiency. Building on the success of Mamba’s learned selectivity mechanism, which empirically improves SSM performance, SeRpEnt provides a formal analysis of selectivity, demonstrating that the learned time intervals in Mamba serve as linear approximators of the information content contained in the sequence elements. This insight lays the foundation for SeRpEnt’s key innovation: a selective resampling mechanism that compresses sequences by aggregating elements based on their informational relevance.

The SeRpEnt framework introduces a novel approach to compress and process sequences by leveraging a selective resampling mechanism that identifies and retains the most informative elements. By dynamically learning the informational relevance of sequence elements through time intervals, SeRpEnt compresses input sequences into shorter representations that are processed at multiple scales to efficiently capture both short- and long-range dependencies. This information-aware compression allows SeRpEnt to enhance the expressiveness of state space models (SSMs) while maintaining computational efficiency.

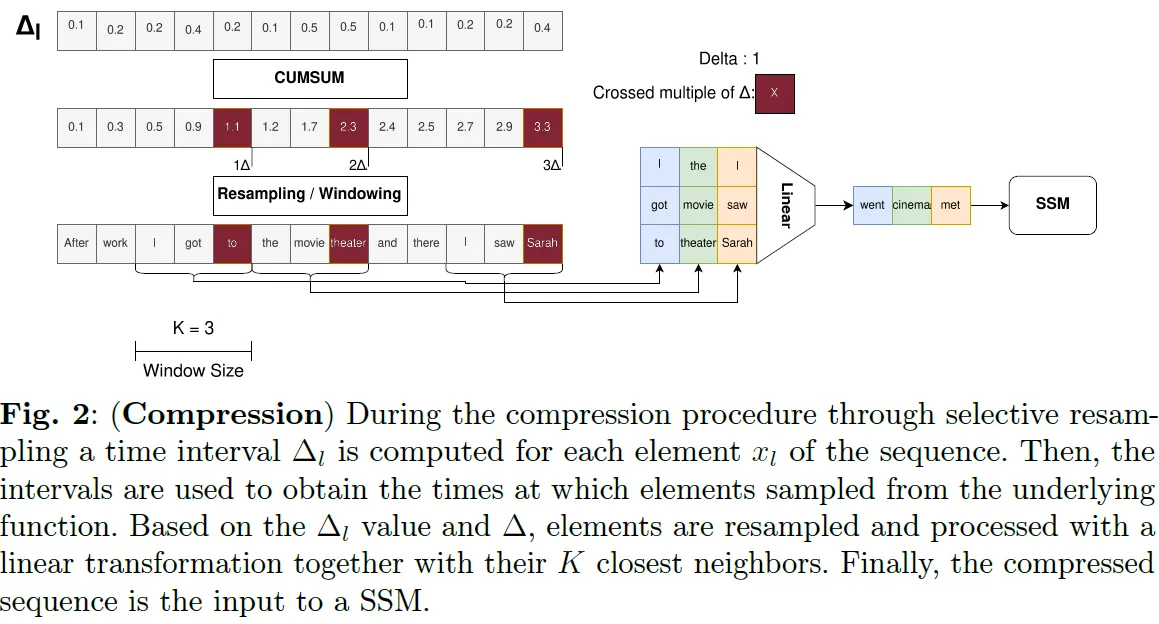
The novel selective resampling mechanism operates by resampling sequence elements at intervals proportional to their learned time intervals ($\Delta_l$), which reflect their contribution to the overall information of the sequence. Resampled sequences are represented with a constant time interval and interpolated using a nearest-neighbors approach. Here’s how it works:

1. Learned Time Intervals as Information Proxies: In Mamba, the time intervals $\Delta_l$ are dynamically learned during training and reflect the importance of each sequence element ($x_l$). Larger $\Delta_l$ values indicate elements that contribute more unique information to the overall sequence, while smaller $\Delta_l$ values suggest redundancy or lower significance. SeRpEnt formalizes this understanding, showing that these intervals can be treated as linear approximators of the element’s informational content.
2. Resampling Process: The sequence $\{{x_l}\}_{l\leq L}$ is resampled into a compressed version $\{{\tilde{x}_l}\}_{l\leq L}$ using the learned $\Delta_l$. The resampling aligns the elements onto a uniform time grid with a fixed interval $\Delta$, aggregating elements that fall within the same resampling window. Since the original sequence’s continuous function $x(t)$ is generally not directly accessible, SeRpEnt uses a nearest-neighbors interpolation approach to infer the values of resampled elements $\tilde{x}_l$ based on their neighbors in the input sequence.
3. Compression Control: The compression rate is controlled by a hyperparameter $\kappa$, which determines the minimum and maximum time intervals for the resampled sequence. This ensures that the compressed sequence retains sufficient information while reducing the number of elements. For example, $\kappa$ guarantees that the compressed sequence has at least $\kappa L$ elements, providing a balance between computational efficiency and informational fidelity.


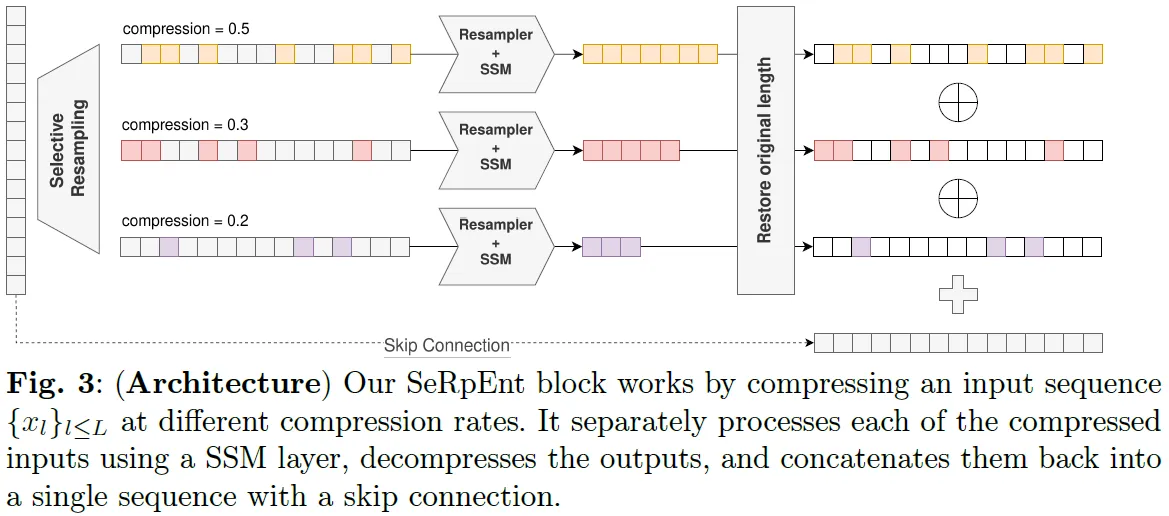
4. Parallel Compression Rates: SeRpEnt processes sequences at multiple compression rates ($\kappa$) in parallel, enabling it to capture both short- and long-range dependencies. Each compressed sequence is passed through a separate SSM, allowing the model to specialize in different scales of information. The outputs of these SSMs are later decompressed and combined, restoring the original sequence length while preserving the essential information captured during compression.
5. Reverse Resampling: After processing, the compressed sequences are decompressed back to the original sequence length. This reverse resampling operation ensures that the model can output results consistent with the original sequence’s temporal resolution, using interpolation techniques similar to those in the compression step.

SeRpEnt extends SSMs like Mamba and S4, offering an orthogonal architectural component for tasks involving long-range dependencies. Empirical results on the Long Range Arena benchmark and language modeling tasks show that SeRpEnt consistently improves the performance of baseline models, especially in sequence classification and language modeling. Notably, it effectively compresses sequences without sacrificing essential information, enhancing both computational efficiency and model expressiveness.

This work is more theoretical than prior advancements in SSMs, providing a rigorous analysis of the mechanics of learned selectivity while introducing a compression and resampling mechanism grounded in information theory. SeRpEnt represents a significant step forward in understanding and optimizing the capabilities of SSMs, with implications for future architectures designed to process long and complex sequences efficiently.